Octal Converter

Created on 8 November, 2025 • Converter Tools • 2 views • 2 minutes read

The Octal Converter is an essential digital tool for anyone dealing with number systems—whether in education, programming, or electronics. It simplifies conversions between octal, binary, decimal, and hexadecimal formats with just a click.

Octal Converter – Convert Numbers Easily Between Octal and Other Systems

Understanding how number systems work is essential in computer science, programming, and digital electronics. One such important system is the octal system, which uses base 8. To simplify conversions between octal and other number systems like binary, decimal, or hexadecimal, a tool called an Octal Converter is used. This article explores what an octal converter is, how it works, and why it’s useful.

What is an Octal Converter?

An Octal Converter is an online or software-based tool that allows users to convert numbers from the octal (base 8) system to other systems, such as decimal (base 10), binary (base 2), or hexadecimal (base 16), and vice versa.

In the octal number system, digits range from 0 to 7. Each octal digit represents three binary digits (bits), making it a compact way to represent binary data. For instance, the binary number 101010 is equivalent to the octal number 52.

An octal converter performs these conversions instantly, helping students, programmers, and engineers save time and avoid calculation errors.

How Does an Octal Converter Work?

The octal converter uses mathematical formulas or built-in programming logic to perform accurate conversions between number systems. Here’s how it typically works:

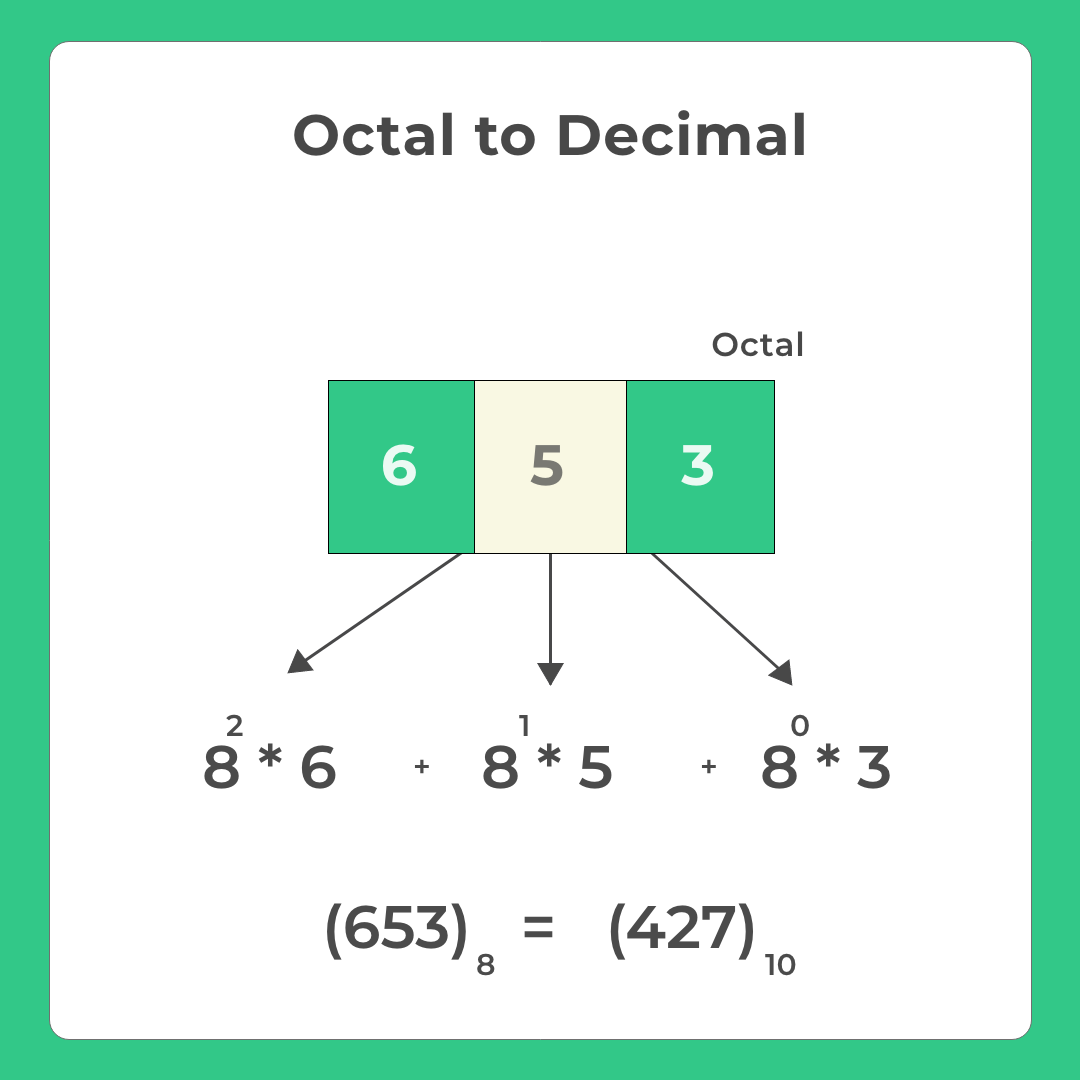
1. Octal to Decimal Conversion

To convert octal to decimal, multiply each digit by 8 raised to the power of its position (starting from right to left, beginning with zero).
Example:
Octal number = 125
Calculation: (1×8²) + (2×8¹) + (5×8⁰) = 64 + 16 + 5 = 85 (decimal)

2. Decimal to Octal Conversion

To convert from decimal to octal, repeatedly divide the decimal number by 8 and record the remainders. The octal number is formed by reading the remainders from bottom to top.

3. Octal to Binary Conversion

Each octal digit can be directly represented by three binary digits.
Example: Octal 47 = Binary 100111

4. Binary to Octal Conversion

Group the binary digits in sets of three from right to left, then convert each group to its octal equivalent.

An online octal converter automates all these steps instantly with high precision.

Why Use an Octal Converter?
1. Speed and Accuracy

Manual conversions can be time-consuming and error-prone. An online octal converter provides instant and accurate results.

2. Useful for Programmers and Engineers

In digital systems, octal representation is often used for simplifying binary data. Converters help professionals quickly switch between systems for analysis or debugging.

3. Educational Benefits

Students learning computer science can use octal converters to understand how number systems interact and practice conversions easily.

4. Cross-Platform Compatibility

Most online converters are compatible with computers, tablets, and smartphones, making them accessible anywhere.

Conclusion

The Octal Converter is an essential digital tool for anyone dealing with number systems—whether in education, programming, or electronics. It simplifies conversions between octal, binary, decimal, and hexadecimal formats with just a click. By understanding how it works and using it effectively, users can save time, enhance accuracy, and deepen their knowledge of computer number systems.

In short, an octal converter bridges the gap between complex numerical systems and everyday computing needs, making it an indispensable tool in the digital age.